Laplace's Theorem

Let $G$ be a finite group with $n$ elements, and $H$ a subgroup of $G$ with $m$ elements. Then $m$ is a divisor of $n$: for a finite group, the order of any subgroup divides the order of the group.

An immediate consequence: If the number of elements in $G$ is prime, then $G$ has no non-trivial subgroup (that is, its only subgroups are ${e}$ and $G$ itself, where $e$ is the neutral element of the group).

This theorem is the first truly “non-trivial” theorem of abstract algebra: it is surprising, simple, and powerful, and evidence that group theory is more than just a “collection of definitions”.

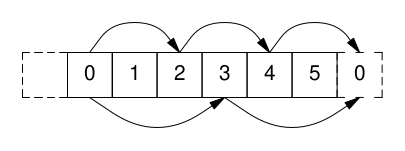
It is, in some sense, also very intuitive. The figure below shows the cyclic group $\mathbb{Z}_6$ of integers modulo 6, and its two possible subgroups, of order 2 and 3, respectively. Clearly, no other subgroups would be able to “close” on themselves as required.

Proof

The standard proof is based on the notion of a coset and two of their properties.

Cosets: Let $a \in G$ be any element of $G$. Then $aH = \{ ah \, | \, a \in G, h \in H \}$ is the (left) coset of $G$. Because $H$ has $m$ elements, $gH$ can have at most $m$ elements. Because no two elements of a coset coincide, each coset has at least $m$ elements; hence all cosets have $m$ elements. (To see the second property, assume the opposite: $g h_1 = g h_2$, with $h_1, h_2 \in H$. Now operate with the inverse $g^{-1}$ from the left and conclude that two elements of a coset are equal only if they are generated by the same element of the subgroup.)

Partition of G: Every element of the group $G$ is the member of at least one coset: $g \in gH$ (because the neutral element $e \in H$ and $e g = g$). Moreover, every element of $G$ is the member of at most one coset. (Assume $c \in aH$ and $c \in bH$ for $a, b, c \in G$ and $a \neq b$. This means that there is an $h \in H$ such that $b h = c$, or $b = c h^{-1}$ which is an element of $aH$ because, by construction, both $h \in aH$ and $c \in aH$. In other words, an element can only be an element of two cosets if the cosets coincide.)

We now have established that every element of $G$ is element of exactly one coset, and that every coset has the same number of elements. In other words the cosets partition the elements of $G$ into a collection of equal-sized subsets, each of which has $m$ elements. We therefore conclude that the number $n$ of elements of $G$ is an integer multiple of $m$, the number of elements in the subgroup $H$.

Personally, I find the proof based on cosets strangely unintuitive, but I am not aware of a substantially different one.