Queueing and Occupancy: The Linear Case
Imagine a parking lot, consisting of a long, linear strip of slots. Cars enter at one end and leave by the other. Let’s also stipulate that each arriving car takes the first available slot that it encounters, that is, it will park in the first empty slot that is nearest to the parking lot entrance. Cars arrive randomly, with a given, average interarrival time $\tau_A$. Furthermore, cars occupy each slot for a random amount of time, but all with a common average dwell time $\tau_D$.
If we number the slots, starting at the entrance, we may now ask the question: what is the probability that the slot with index $n$ is occupied?
Simulation
The problem calls for a simulation. The implementation is “event-driven”, which (in a simulation context) means that future “events” (such as cars arriving or departing) are pushed onto a queue. Events are then picked off of the queue in their order of occurrence and processed. The priority queue required for such a processing model is conveniently provided by a heap data structure.
(An aside: the heap data structure in the Go standard library provides
an interface, containing functions Push() and Pop() that must be
implemented by the client code. However, these functions are only for
the package’s internal use! Client application code instead must use
the package-level functions of the same name: heap.Push() and
heap.Pop(). Getting this wrong will not be detected at compile time
and lead to mysterious runtime errors.)
The implementation uses the exponential distribution $p(t) = \lambda e^{-\lambda t}$ to generate both arrival and departure epochs. Here, the parameter $\lambda$ corresponds to the arrival or departure rate: $\lambda_\text{arrival} = 1/\tau_A$ and $\lambda_\text{departure} = 1/\tau_D$. Furthermore, in the implementation we will fix $\tau_A = 1$, so that the dwell time is the only varying parameter. Put differently, we measure dwell time in multiples of the average interarrival time.
The occupancy of each slot is recorded at fixed intervals; the frequency with which each slot is occupied is shown below.
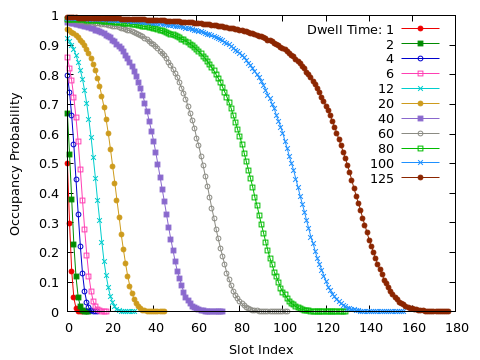
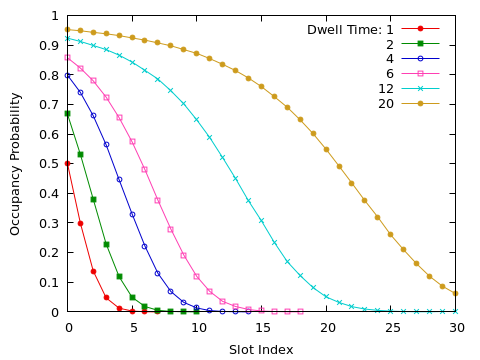
Modeling
The results certainly make intuitive sense. They also display a certain kind of regularity. Can we find a simplified description (a “model”) to explain the occupation probability, for each slot, in terms of the external parameter $\tau_D$?
A first step is the realization that the system constitutes an M/M/∞ queue (in Kendall’s notation): arrivals are exponentially distributed, dwell times (i.e. service times) are exponentially distributed, and there is an essentially infinite number of servers (i.e. slots). Queueing systems are usually described in terms of arrival and departure rates; to make contact with the relevant theory we identify:
\begin{align*} \text{Arrival rate} && \lambda = 1/\tau_A \\ \text{Departure rate} && \mu = 1/\tau_D \end{align*}
For such a system, the mean number of occupied slots is $\lambda/\mu$. (This is easy to see: consider how the number of cars changes over a short time interval $dt$: $n(t + dt) = n(t) + \lambda dt - \mu n(t) dt$. This takes into account that each of the $n(t)$ cars that are currently parked may leave with probability $\mu dt$, but that at most one car will arrive, with probability $\lambda dt$. This expression leads to a differential equation $\dot{n(t)} = \lambda - \mu n(t)$. In the steady state, the left-hand-side is zero, leading to $n(t) = \lambda/\mu$.)
Moreover, when the dwell time is much larger than the interarrival rate (so that $\mu \ll \lambda$), the number of occupied slots is Gaussian distributed, with $m = \lambda/\mu$ and $\sigma = \sqrt{\lambda/\mu}$. In other words, the probability to find $n$ slots occupied is:
\[ p(n, \lambda, \mu) = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left( -\frac{1}{2} \left( \frac{n - m}{\sigma} \right)^2 \right) \qquad \text{with $\quad m = \frac{\lambda}{\mu} \quad$ and $\quad \sigma = \sqrt{\frac{\lambda}{\mu}}$} \]
If we identify the observed occupation frequency with $p(n, \lambda, \mu)$, then we expect that $\sigma \cdot p(n, \lambda, \mu)$ equals $e^{-z^2/2}/\sqrt{2 \pi}$, for $z = (n-m)/\sigma$, independent of $\lambda$ and $\mu$. Put differently, we expect the data points for all values of $\lambda$ and $\mu$ to collapse onto a single curve. This is indeed the case, as shown in the following figure.
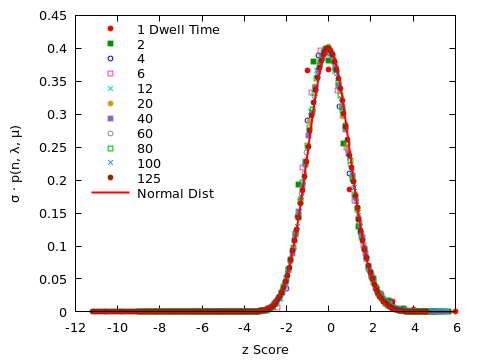
The foregoing analysis does apply only to the total number of occupied slots in the lot, it does not take their spatial arrangement into account. In particular, it disregards the requirement that new arrivals always take the first slot available to them. Nevertheless, guided by the previous result, we plot the occupation frequency for each slot, as a function of the $z$-score $z = (n-m)/\sigma$. Again, the collapse is almost perfect; only for relatively short dwell times ($\tau_D \le 6$), do we observe appreciable deviations.
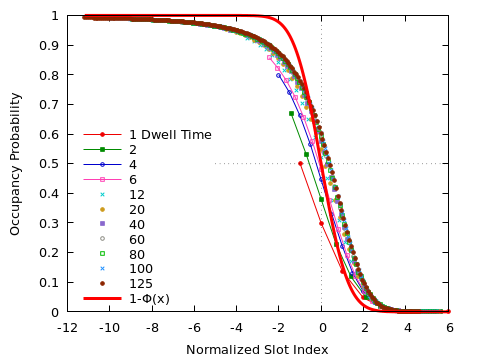
It is worth understanding the meaning of the $z$-score in this example. The variable $z$ measures the distance of a slot from the mean fill level for the given value of $\tau_D$ (rather than from the entrance of the parking lot). Furthermore, the distance from this new origin is measured in terms of the typical “width” of the transition region between the filled and empty parts of the lot.
For comparison also shown is $1 - \Phi(x)$, where $\Phi(x)$ is the cumulative distribution function of the standard normal: \[ \Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^x \, \exp \left( - \left( \frac{x}{2} \right)^2 \right) \]
Although having approximately the same shape, this function clearly does not describe the data well. In particular, the function is has odd symmetry, whereas the data is clearly not symmetric about the origin. This is where the requirement that arriving cars take the first slot available to them becomes relevant!