A Mathematical Mystery

In my previous post on one-dimensional heat flow, I encountered sums of the form:

$$ \sum_{n=0}^\infty \frac{\pm 1}{2n+1} \exp \left( - (2n+1)^2 x \right) $$

A plot (involving the first 1000 terms) is shown below, and looks reasonable enough. Is this curve, which forms the limit of the series, a known function?

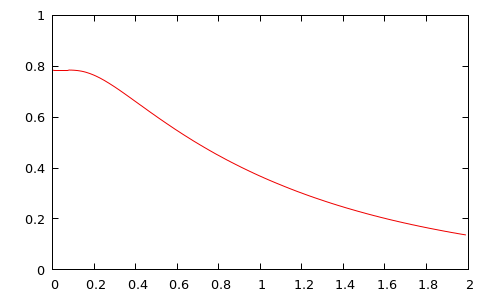
Near $x=0$, the curve seems flat, possibly even “infinitely flat”; one would expect the function to have zero derivative as $x \to 0$. Yet, differentiating the sum term-by-term, and setting $x=0$, leads to:

$$ \sum_{n=0}^\infty \mp (2n+1) $$

which most definitely does not converge (in any conventional sense), and surely does not equal zero.

The situation is a bit subtle. The original series converges only conditionally for $x=0$, but does converge absolutely for any $x>0$, because the later terms in the sum are exponentially small. Hence, it should come as no surprise that term-by-term differentiation is not valid at the origin.

Nevertheless, It is not clear how to obtain the proper behavior for small $x$. A Taylor expansion does not seem useful. Would an analytic continuation into the complex plane be helpful? Is there an obvious regularization or resummation method to apply?

Numerically, the behavior is quite stable, even when truncating the series after only a few terms. The reason is that the individual terms in the sum are exponentially small for any $x$ of reasonable size, so that the sum is dominated by the $n=0$ term for such $x$. Yet this does not explain the near perfect cancellation of terms for small $x$.

Overall, I have the impression that this should be a “well-known” problem. Yet, I don’t recall ever seeing sums of this form before. Which is strange, given how regular the formula is — surely, someone must have studied this problem before!